輪郭部の方向性を考慮した高速重心計算

これは、1998年（平成10年）10月に大分大学で行なわれた電気関係学会九州支部連合大会で発表した内容についてのページです。実際には、この理論についての話をする少し前の平成10年７月に、鹿児島県の霧島ハイツというところで、情報処理学会九州支部の「若手の会」という自由発表の場で話をさせていただいたことがありました。ただし、この「若手の会」では、輪郭部分のデータを追跡するだけで、重心を求める理論的な話について、片側方向の輪郭追跡についての話をしました。このときには、面積を求める部分で、まだ高速化の余地が残っているのではないかと思いながら話をさせていただきました。

そして、電気関係学会九州支部連合大会では、二次元的に閉じた曲面について、両方向での輪郭追跡について拡張したことと、面積を求める部分の高速化を行い発表させていただきました。この理論に基づいて計算を行った結果をシミュレーターを用いて解説してみたいと思います。

まず、時計回り方向について「大」という文字の重心を求めた結果です。重心位置は赤の×点が付けてあります。

二番目に、時計回り方向について円形の重心を求めた結果です。

三番目に、時計回り方向について四角形の重心を求めた結果です。

四番目に、時計回り方向について三角形の重心を求めた結果です。

五番目に、時計回り方向について六角形の重心を求めた結果です。

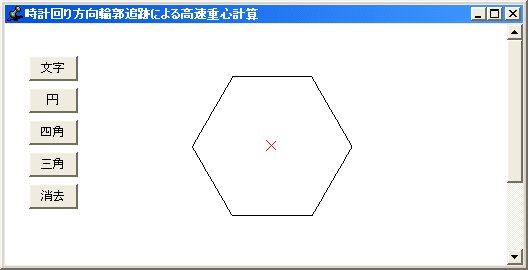
六番目に、時計回り方向について複雑な図形（その一）の重心を求めた結果です。

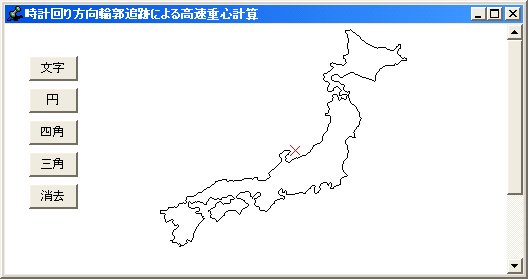
七番目に、時計回り方向について複雑な図形（その二）の重心を求めた結果です。

八番目に、時計回り方向について複雑な図形（その三）の重心を求めた結果です。

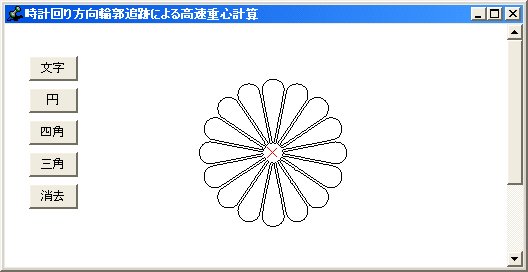
ここまでが、「若手の会」で話をした理論に基づいた計算方法です。その後、輪郭追跡を両方向にまで拡張した理論に基づき反時計回り方向でのシミュレーション結果を示します。

まず、反時計回り方向について「与」という文字の重心を求めた結果です。

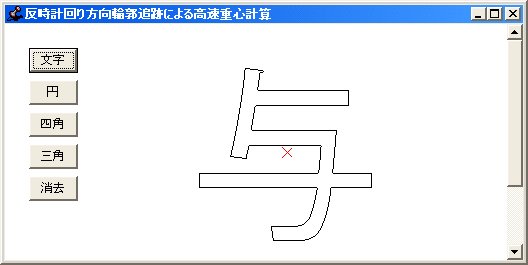
二番目に、反時計回り方向について円形の重心を求めた結果です。

三番目に、反時計回り方向について四角形の重心を求めた結果です。

四番目に、反時計回り方向について三角形の重心を求めた結果です。

五番目に、反時計回り方向について六角形の重心を求めた結果です。

六番目に、反時計回り方向について複雑な図形（その一）の重心を求めた結果です。

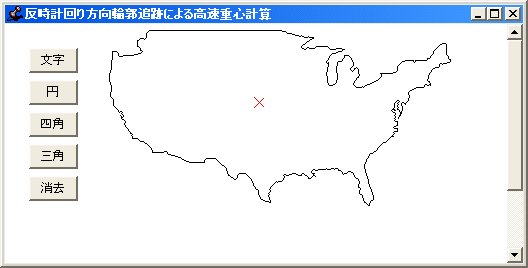
七番目に、反時計回り方向について複雑な図形（その二）の重心を求めた結果です。

八番目に、反時計回り方向について複雑な図形（その三）の重心を求めた結果です。

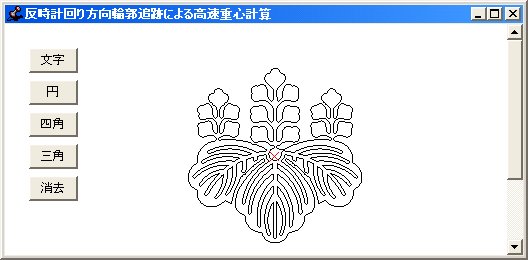
このように、反時計回りの方向でも、方向性を考慮した演算方法を用いることによって、正しい結果が得られることが分かります。

これらの結果により、重要な結論が一つ言えると思います。（少し数学の専門的な話になって恐縮ですが）それは以下のように、ベクトル場Ｈというものの成分を(H1,H2,H3）とします。このときにrot （ローテーション）という演算は、方向性を考えて次のように複合同順に演算をしないと、正しい結果を導くことができないという証拠の一つであるということです。

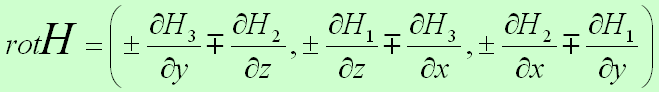
それでは最後に、この重心計算理論の社会で利用されることについては、くれぐれも平和的な有効利用がなされることを切に望んでいることを一言申し添えておきたいと思います。

一般に数学的な座標系においては、左下が原点となっていますので、Ｘ方向は右にいくほど大きくなり、Ｙ方向は上にいくほど大きくなります。一方、パソコン画面では、左上が原点となっているのが普通です。従ってＸ方向は右にいくほど大きくなりますが、Ｙ方向は下にいくほど大きくなります。このため、通常の数学の世界で定義されたrot の回転方向と、この高速重心計算理論で述べている回転方向は逆になっています。

二次元上で閉じた形の輪郭追跡とは、あくまでも閉じた閉曲面の外側から、輪郭点列をすべて含む状態で追跡した場合のことであって、閉じた閉曲面の内側から輪郭を追跡することではありません。

シミュレーションの結果、表示された赤の×点は整数であるパソコン画面の点の上にしか描くことができませんが、実際の演算結果は少数点以下まで正しく計算されていることを確かめております。

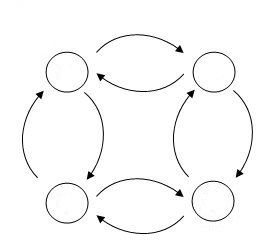
この理論の構築において、基本的なアイデアのヒントとなった図があります。それは参考資料「オートマトン・言語理論　本多波雄著　コロナ社　1972」における下記のような状態遷移図であったことも付記しておきたいと思います。

二次元の閉曲面について輪郭の追跡方法の基本的なアイデアは、右手探索（左手探索）と呼ばれているもので、建物の壁に右手（左手）を沿わせて歩けば建物を一周して戻ってくることができるという考えです。右手探索は時計回り方向の輪郭追跡で、左手探索は反時計回り方向の輪郭追跡ともいえます。どちらも具体的には３×３のマスクパターンを用いて追跡を行うのが一般に広く使われている手法となっているようです。


時計回り３×３マスク	反時計回り３×３マスク

上図のように、各マスクの数字は方向を表します。また、高速重心計算の輪郭データは、二連結の中点座標を利用します。これは下の図例（時計回りの場合）のように二連結の中点から見て、前からの連結と次への連結を数字で表します。さらにこのときの中点についてのベクトルを輪郭追跡と共に記録していきます。

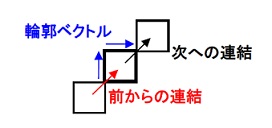
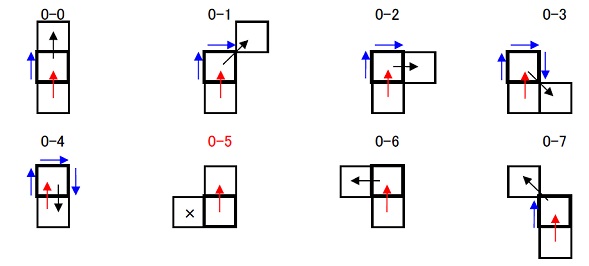
２連結の中点について、前からの方向と次への方向の組み合わせを考えると64通りあります。このとき下図のように前からが上方向の場合、次への連結は８通りありますが、１つだけ起こりえない方向連結があります。これを全方向について調べてみると前からの方向を基準にすると必ず５つ進んだ（３つ戻った）方向があり得ない方向連結となっています。従って中点座標から次への方向を調べるためには６つ進んだ（２つ戻った）方向から数字の順番に調べれば次への連結方向が分かり、３×３のマスクを移動させて輪郭追跡を行うことができます。

このようにして輪郭追跡を行い、半楕円と四角形（１辺の長さが51）の閉曲面の重心座標と周囲長を求めた結果を以下に示します。Gx、Gy、赤い×印は重心の座標で、黒い×印は輪郭追跡の始点座標です。LENは輪郭の周囲長を表示しています。周囲長については各種定義があるようですが、ここでは二連結の中点の辺を合計したもので、正方格子で構成された正確な図形の輪郭周囲長です。


半楕円の閉曲面（時計回り）	半楕円の閉曲面（反時計回り）


四角形の閉曲面（時計回り）	四角形の閉曲面（反時計回り）

さらに二連結の中点を用いて輪郭追跡を行う利点として、次のように直線と四角形が接合したような平曲面で、輪郭追跡の始点が直線の途中から始まっているような場合があります。このような場合でも正確に輪郭追跡を行います。


（時計回り）	（反時計回り）

極端な話ですが、直線のみや文字フォントのような直線で構成した文字でも輪郭追跡と周囲長、重心計算を行うことができます。


直線のみ（時計回り）	直線のみ（反時計回り）


直線で構成した文字（時計回り）	直線で構成した文字（反時計回り）

高速重心計算アルゴリズムの処理速度を実際のPC上で計測してみました。システムはIntel Corei3-330M（2.13GHz）搭載のTOSHIBA SATELITE L40でOSはWindows7（Pro）です。今回のプログラムはC++Builder5という少々古い開発システムのため、WindowsXP-MODEというエミュレーションモード上で動かしました。

計測用の閉曲面には、1024×512の長方形（周長3072、閉曲面内部のピクセル数524,288）を描画して、その重心を計算するときの処理時間を計ってみました。時間計測にはC++Builderに備わっているプロセッサ時間を求めるclock()という関数を利用しました。このタイマーの精度は1msec程度ということらしいです。タイマーのスタートとストップはプログラムの中で下図のような個所に挿入しました。

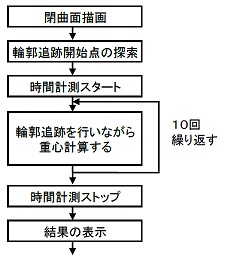
また、１セットの計測は同じ輪郭追跡と重心計算の部分を10回繰り返して行い、これを10で割ったものを１セットの実測値としました。そしてこの実測を10セット行った結果、やはりマルチタスクのOSで動作させるせいか、同じ閉曲面図形の計測でも13msec～40msecとバラつきがありました。これを単純に平均すると22.1msec（ミリ秒）という参考値が出ました。

やはり正確に測定するためには、シングルタスクのシステムで精度の良いタイマーを用いて行うべきですが、PCソフトシミュレーターとしてはこの程度の計測が限界ではないでしょうか。また、さらなる高速化については、汎用プロセッサの命令セットでは見かけませんが、信号処理専用プロセッサなどに備わっているような、掛け算と加算を１~~クロック~~サイクルで同時に行うMULADD命令をもったプロセッサなどを利用することも有効な手段ではないかと思われます。

学会でも質問されたことですが、この計算法の三次元への応用について少し説明しておきたいと思います。

三次元への応用について一番難しいところは、重心の計算法というよりも、三次元の閉曲面上をどのように探すかということがネックになっているのではないかと考えております。

二次元の場合には、複雑な図形であっても、閉曲線であれば一筆書きのように曲線全体のつながりを探索する手法があります。しかし、三次元の場合には、どのような複雑な曲面であっても、一筆書きのような面を探索する手法が存在するのかどうかということが問題ではないでしょうか。（私も数学における位相幾何学の専門家ではありませんので、存在するかどうかについては分かりません[追記１を参照のこと]）

やはり三次元重心計算の実用化という観点から考えますと、三次元の曲面体を薄く輪切りにして、その厚み（ここでは仮にＺ方向とします）を計算の最小単位（計算機空間上の１ピクセルなど）にしておけば、それぞれの厚みの重心はピクセルの場合、ピクセルの半分がＺ方向の重心となります。

そして、輪切りにしたＸ─Ｙ面上で、高速重心計算をすれば、Ｘ方向の重心とＹ方向の重心、および体積（ピクセルの個数）が分かりますので、Ｚ方向のモーメント（Ｚ方向の重心と体積を掛け合わせたもの）も分かります。従って、これら輪切りにしたものすべてを最後に合わせると、三次元上の重心が計算できるのではないかと考えておりますが、文章で書くと長くなりますので、この話題はこれくらいにしておきます。

この理論では、ＸＹ計算機座標系において、Ｘ方向とＹ方向のモーメントの計算式はそれぞれ数学的に美しい対称形から成っています。また、Ｘ方向のモーメントはＸ軸方向の計算結果だけを考えれば良く、Ｙ方向のモーメントはＹ軸方向の計算結果だけを考えれば良いという特徴があります。

この高速重心計算の理論をつくるにあたって、いくつかの高速化のアイデアが盛り込まれています。その中でもモーメントの計算における数学的な理論をつくるにあたって、当初、積分範囲を原点から原点プラス１までの範囲で考えていました。

しかし、それでは計算結果において、1/2を加える計算式が出てしまいます。実社会でハードなプログラミングの仕事に携わった経験のある方ですと、真に高速化が必要な部分の１コードにおける重要性については、よく分かっておられる技術者の方々も世間には多いのではないでしょうか。

もしこの1/2を加える演算が、輪郭データの個数やデータの連結状況に応じて必要になるとすれば、計算機コードにおけるシフト命令と、加算命令などが輪郭データの個数に応じて増えることが予想されるわけです。これをなんとか加算命令１つで済むように置き換えられないものかと思案しました。それで、この問題を解決するために、次の案が浮かびました。

積分範囲をＸ方向、Ｙ方向のモーメントでは、それぞれ当初のものより、Ｘ方向のモーメントではＸ軸上に-1/2だけ、Ｙ方向のモーメントではＹ軸上に-1/2だけずらし、演算結果に１の加算のみが出るようにします。これにより、加算命令１つで置き換えることができるのではないかということです。

しかし、それにはあらかじめ-1/2だけずらしているので、後でそのずらした分を演算上修正する必要があるというような問題が出ました。このような方法は、理論の単純さという点から、あまり好ましいとはいえないと思い、なんとかこの両方を解決できる良いアイデアはないものかと思案しました。

この理論は連続系で理論を考えて、それを離散座標系の演算に応用しようというものですが、問題解決のヒントとなったものが、連続系と離散系における極めて重要な、染谷－シャノンのサンプリング（標本化）定理というものです。この定理では、標本化関数というものが現れます。これは以下のようにゼロを基準として、マイナス側とプラス側で美しい対称の形になります。

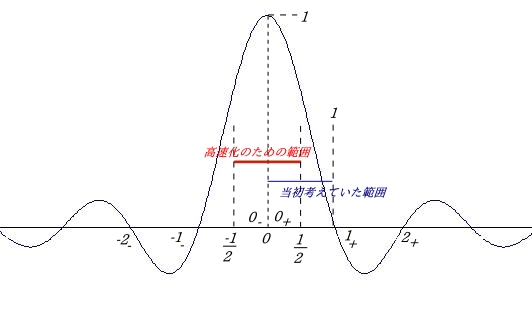
ここで、原点を０として考えますと、０（ゼロ）はプラスでもマイナスでもない特別な数とされています。また、ゼロは無ですから、どんな数にゼロを掛けてもゼロになります。

次に、離散化するときの周期ついては、周期はどれも等しい長さでなければなりません。これらのことを考慮して、高速化にあたっては離散化するときの周期の範囲を次のように考えることにしました。

下付きのマイナス記号は、その数よりもマイナス側に限りなく近い実数、下付きのプラス記号は、その数よりも限りなくプラス側に近い実数としています。

もちろん、無である０が定義できないということではなく、マイナス側からみれば、0_-の極限値として0を定義し、プラス側からみれば、0₊の極限値として0が定義できるものとします。

標本化関数のlimθ→0のとき、sin(θ）／θ→1も極限値として定義されていることは、ご存知の方も多数いらっしゃると思います。そこで、離散化するときのサンプリング周期をマイナス側とプラス側でそれぞれ次のように考えます。

以上のことから、あらかじめサンプリング定理の範囲内で、-1/2だけずらしていますので、連続座標系で理論を考えた後でも、それをそのまま離散座標系に置きかえるだけで、演算の高速化と後処理計算の手間をはぶく、一挙両得になると考えました。

三次元上で一筆書きのように面を探索するアルゴリズムの問題も難しい問題ですが、グラフ理論においても考えてみる必要があるのではないでしょうか。現在でもP≠NP（注）のようです。従って、グラフ理論で一筆書きの経路を発見的探索によって探す場合には、面の数が増えると、探す経路の数が最悪指数関数的に増大することが分かります。有限時間で探索できなければ、まず実現性があるとはいえません。これらの問題がすっかり解決された後で、ガウスの定理を用いて三次元の重心計算理論を考案しても（もし必要があれば）、決して遅くはないと考えています。
（注）P 多項式オーダーの計算量で解ける問題 NP 非多項式オーダーの計算量で解ける問題

この重心計算理論は、あくまでも計算機座標系（左上が原点、Ｘ軸は右方向がプラス、Ｙ軸は下方向がプラス）において理論展開をしています。これは計算機のグラフィック処理系が、原点を左上にとっていることが多いことによるものです。一方、数学座標系は、左下に原点（Ｘ軸は右方向がプラス、Ｙ軸は上方向がプラス）をとっている学術文献が主になっていますので、この重心計算理論を考えるときには、原点の相違による回転方向、算術符号などに注意をする必要があります。

情報処理学会論文資料全般に渡って、日本語文の句読点は「．」（ピリオド）と「，」（カンマ）となっているようです。私も1998年の時点で、決してわざとではありませんが、うっかり句読点を「。」（句点）と「、」（読点）として、原稿を書いてしまいました。これについては、近年の社会における日本語ワードプロセッサーをはじめとする日本語文書処理技術の発展に伴って、何とか読者が読みやすいように、他学会との連携、協議をお願いしたいものだと思っております。

ジョージ・ガブリエル・ストークス（Sir George Gabriel Stokes　1819-1903）

アイルランド出身の数学、物理学者　ベクトル解析におけるストークスの定理、ナヴィエ・ストークスの粘性流体式が有名